Akkumulierende Parameter
Einführung in die Programmierung

Ausgehend von der mathematischen Definition:

\[n! = n \cdot (n-1) \cdot (n-2) \cdot\cdot\cdot 2 \cdot 1 = n\cdot (n-1)!\] kann folgende rekursive Funktionsdefinition gegeben werden:

    (define factorial
       (lambda [n]
          (cond 
             [(= n 1) 1]
             [else (* n (factorial (- n 1)))])))

Die Anwendung (factorial 6) führt zu folgendem rekursiven Abarbeitungsprozess:

\(n! = 1 \cdot 2 \cdot\cdot\cdot (n-1) \cdot n\)

Berechnung der Fakultät im Vorwärtsgang mit zwei Hilfsvariablen:

product \(\leftarrow\) product * counter

counter \(\leftarrow\) counter + 1

product ist gleich \(n!\), wenn counter größer als \(n\) ist.

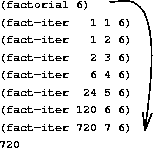
    (define factorial
      (lambda [n]
        (fact-iter 1 1 n)))

    (define fact-iter
      (lambda [product counter max-counter]
        (cond 
          [(> counter max-counter) product] 
          [else (fact-iter (* product counter) 
                           (+ counter 1)
                           max-counter)])))

• Die Funktion fact-iter hat reinen Hilfscharakter, d.h. sollte nur von factorial aufgerufen werden.

• Konsequenz: Funktion fact-iter lokal definieren:

         (define factorial
           (lambda [n]
             (letrec 
                 ([fact-iter
                   (lambda [product counter]
                     (cond 
                       [(> counter n) product] 
                       [else (fact-iter (* product counter) 
                                        (+ counter 1))]))])
               (fact-iter 1 1))))
  

• Das dritte Argument für fact-iter ist überflüssig geworden.

• Ein rekursiver Prozess ist durch eine Folge von verzögerten Operationen gekennzeichnet.
• Der Speicherbedarf für das Merken von noch nicht ausgeführten Operationen wächst linear mit \(n\).
• Die iterative Abarbeitung erfordert hingegen nur konstanten Speicherbedarf für die Werte von product, counter und max-counter.
• product bezeichnet man als akkumulierenden Parameter.
• Akkumulierende Parameter ermöglichen oft die iterative Abarbeitung rekursiver Funktionen.
• Akkumulierende Parameter führen oft zu effizienteren Funktionen.

• Vorbemerkung: Beide Funktionen entstehen durch Anwendung der bekannten Regeln für den Entwurf listenverarbeitender Funktionen.
• putatend wird \(n\) mal rekursiv aufgerufen, wenn \(n\) die Mächtigkeit der Liste ist, d.h. cons wird \(n\) mal ausgeführt.
• rev-list ruft sich selbst ebenfalls \(n\) mal auf.
• Jeder Aufruf von rev-list ruft einen Aufruf von putatend hervor.
• Für diese Aufrufe von putatend ist die Länge des zweiten Arguments \(n-1, n-2\ldots 1, 0\).
• Die Anzahl der cons-Aufrufe von putatend beträgt: \[0 + 1 + \cdots + n-1 = \frac{n(n-1)}{2}\]
• Die Funktion rev-list wächst quadratisch: \(O(\texttt{rev-list})=n^2\).

• Das Invertieren einer Liste sollte aber nur linearen Aufwand erfordern.
• Lösung: Hilfsfunktion mit akkumulierendem Parameter

    ;; kehrt die Reihenfolge der Symbole einer Liste um
    ;; rev-list (list-of symbol) -> (list-of symbol)
     (define rev-list
      (lambda [list]
        (letrec
            ([rev
              (lambda [list-x list-y]
                (cond 
                  ((empty? list-x) list-y)
                  (else (rev (rest list-x) 
                             (cons (first list-x) 
                                   list-y)))))])
          (rev list empty))))

• Die Anzahl der cons-Aufrufe in rev wächst linear mit der Länge der Liste.

• Im Zusammenhang mit akkumulierenden Parametern sind zwei Fragen interessant:
  1. Woran erkennt man, dass eine Funktion von akkumulierenden Parametern profitieren kann?
  2. Was muss ggf. in einem akkumulierenden Parameter eigentlich akkumuliert werden?
• Schwierigkeit beim Entwurf einer solchen Hilfsfunktion: Die bekannten Regeln sind nicht ohne weiteres anwendbar.

• Da war zunächst die Frage, ob eine Funktion mit akkumulierendem Parameter zweckmäßig ist.
• Frage ist i.a. nicht leicht zu beantworten.
• Indiz: Die Anwendung der bekannten Regeln liefert eine Funktion, die die Liste rekursiv abarbeitet unter Verwendung einer Hilfsfunktion, die die Liste ebenfalls rekursiv abarbeitet.
• Hier ist eine Effizienzbetrachtung angebracht.
• Vergleiche die Definition von rev-list mit Hilfsfunktion putatend.
• Der Entwurf einer Hilfsfunktion mit akkumulierendem Parameter vollzieht sich dann in zwei Schritten:
  1. Man schreibt zunächst eine Funktionsschablone für die Funktion samt lokaler Hilfsfunktion mit akkumulierendem Parameter auf. Siehe nächste Folie!
  2. Man beschreibt präzise die Aufgabe des akkumulierenden Parameters durch eine so genannte Akkumulatorinvariante. Siehe übernächste Folie!

    (define rev-list
      (lambda [list]
        (letrec
            ([;; Akkumulator ...
              rev
              (lambda [listX akku]
                (cond 
                  [(empty? listX) ... akku ...]
                  [else 
                   ... (rev (rest listX) 
                            ... (first listX) ...akku)
    ;;                      ==========================
                            ]))])
          (rev list ...))))

• Das Argument für den akkumulierenden Parameter im rekursiven Aufruf der lokalen Hilfsfunktion rev ist hier unterstrichen.
• Es muss so bestimmt werden, dass die noch zu definierende Akkumulatorinvariante gültig bleibt.

• Eine Akkumulatorinvariante ist eine Aussage über das Argument der Hauptfunktion (hier: list), das entsprechende Argument der Hilfsfunktion (hier: listX) und den Akkumulator, die vor und nach jedem rekursiven Aufruf der Funktion gilt.
• Für den letzten Aufruf von rev gilt: \(listX = empty\). Wenn wir voraussetzen, dass akku dann das invertierte list enthält, können wir die Schablone für den Fall, dass das Argument listX von rev empty ist, so ergänzen: [(empty? listX) akku].
• Für den ersten Aufruf von rev gilt: \(listX = list\). Da beim Invertierungsprozess keine Listenelemente hinzukommen, kann die Schablone hier so ergänzt werden: (rev list empty)

• Da bei jedem rekursiven Aufruf von rev vorne ein Element von listX wegenommen wird, muss (first listX) an den Anfang der Liste akku gestellt werden. Damit ergibt sich für den unterstrichenen Teil der Schablone: (cons (first listX) akku)).
• Akkumulatorinvariante: akku ist eine Liste, die diejenigen Elemente von list in umgekehrter Reihenfolge enthält, die denen von listX vorangehen.